Anaxagore-Eratosthène


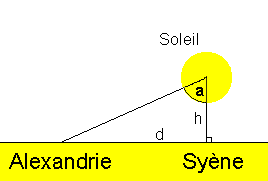
Vers l'an 430 avant Jésus-Christ, le philosophe grec Anaxagore avait calculé que le Soleil, une petite boule de feu de 60 km de diamètre, flottait dans l'air à 6500 kilomètres.

Son raisonnement avait pour point de départ le fait suivant : des voyageurs revenant de la ville de Syène, près du Nil, lui avaient appris que le jour du solstice d'été, à midi, le Soleil était au zénith et que les objets n'avaient pas d'ombre. Plus tard, il apprit que le Soleil, le jour du solstice d'été, faisait un angle de 7° avec la verticale à l'emplacement de la future Alexandrie, à 800 km au nord de Syène.
A cette époque, on pensait que la Terre était plane. D'où la figure ci-dessus.

tan a = d / h donc h = d / tan a = 800 / tan 7 = 6515 km.
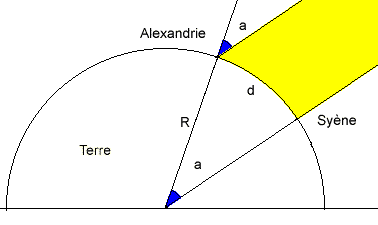Il déduisit le diamètre du Soleil, 60 km, de son diamètre apparent, qui vaut 1 demi-degré. Ces résultats sont très loin de la réalité puisque le Soleil est à 150 millions de km et que son diamètre vaut 1,39 millions de km.


Malgré des mesures correctes, l'hypothèse d'Anaxagore était fausse, ses résultats aussi.
Deux siècles plus tard, un autre philosophe grec, Eratosthène, reprit les mêmes observations, mais il apporta deux hypothèses complètement différentes :
- le soleil était très éloigné de la Terre, de telle sorte que ses rayons arrivaient parallèlement entre eux.
- la Terre était sphérique.

La figure est différente. L'angle d'inclinaison du Soleil par rapport à la verticale est a.
Ci-dessus, on trouve que le rayon R = d / a, avec a = 7° = 7 * 3.14 /180 radians.
Ici, R = 800 /(7*3.14/180) = 6551 km. Ce résultat est très proche de la valeur connue actuellement, 6378 km en moyenne.

C'est cette mesure de R que l'on se propose de faire aujourd'hui.